Factorial

Table of contents

  1. Full Factorial
  2. References
  3. Version History

Full Factorial

A Full Factorial DoE is a comprehensive method used in experimental research to investigate all possible combinations of factor levels, allowing for a complete analysis of two or more factors. Each factor is tested at different discrete levels, and the total number of experimental combinations ($n$) is determined by multiplying the number of levels ($l_f$) of each factor ($f$). This relationship is mathematically expressed as:

$$ \begin{equation} n = \prod_{f=1}^{F} l_{f} {\qquad [1] \qquad} \end{equation} $$

where, $n$ is the number of total experimental combinations, $F$ is the total number of factors and $l_f$ is the number of levels of the $f$ factor.

The strength of Full Factorial DoE lies in its thoroughness. By examining every possible combination of factors and their levels, it provides a detailed mapping of the experimental space. This design is particularly powerful for elucidating not only the individual effects of each factor but also any interactions between them. Such interactions can often be critical, influencing the outcome in ways that would not be evident from studying the factors independently.

Full Factorial DoE ensures that every potential interaction is explored, offering a robust understanding of the system under investigation. This is crucial for drawing reliable conclusions and making informed decisions based on the experiment’s results. However, while Full Factorial DoE is unmatched in its comprehensiveness, it can become extremely resource-intensive, especially as the number of factors or levels increases. Each additional factor exponentially increases the number of experiments needed, which can escalate costs and time requirements significantly.

Thus, while Full Factorial DoE provides an unmatched depth of understanding due to its exhaustive exploration of all factor combinations, its practical application must be carefully considered.

Balancing the need for comprehensive data with the practical limitations of experimental resources is essential. In cases where resources are limited or the number of factors is high, alternative designs like fractional factorial designs or response surface methodologies might be employed to efficiently capture the most critical information without conducting every possible experimental combination.

Use the Full Factorial function by browsing in the top ribbon:

DOE \(\rightarrow\) Factorial \(\rightarrow\) Full Factorial

Input

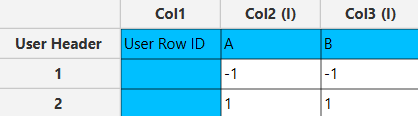
Numerical values should be specified in the input datasheet. The minimum requirement is to specify 2 columns (factors) along with two levels (values/rows) each representing min and max levels, respectively.

Configuration

Number of Center Points Select manually the Number of Center Points to be included in the output list of experiments. There is no minimum requirement or any other limitation.
Number of Blocks Select manually the Number of Blocks. The lowest value that can get is 1.
Random Standard order You can tick/select the box if randomness is required in the output list of experiments.
Time-based RNG Seed If randomness is selected, then you have the option to also tick/select the box to set the random generated number seed based on time.
RNG Seed Select manually the random generated number seed if required.
Include/exclude columns Select manually the columns through the dialog window: Use the buttons to move columns between the Included Columns and Excluded Columns list. Single-arrow buttons will move all selected columns and double-arrow buttons will move all columns.

Output

A list of experiments (combinations) is generated in the output datasheet along with the Block number and the Standard order based on the Full Factorial design method selected.

Example

Input

In the input datasheet minimum requirement is to specify two factors (columns) and insert minimum two levels (values) for each factor (column), as shown below.

Full Factorial input
Configuration
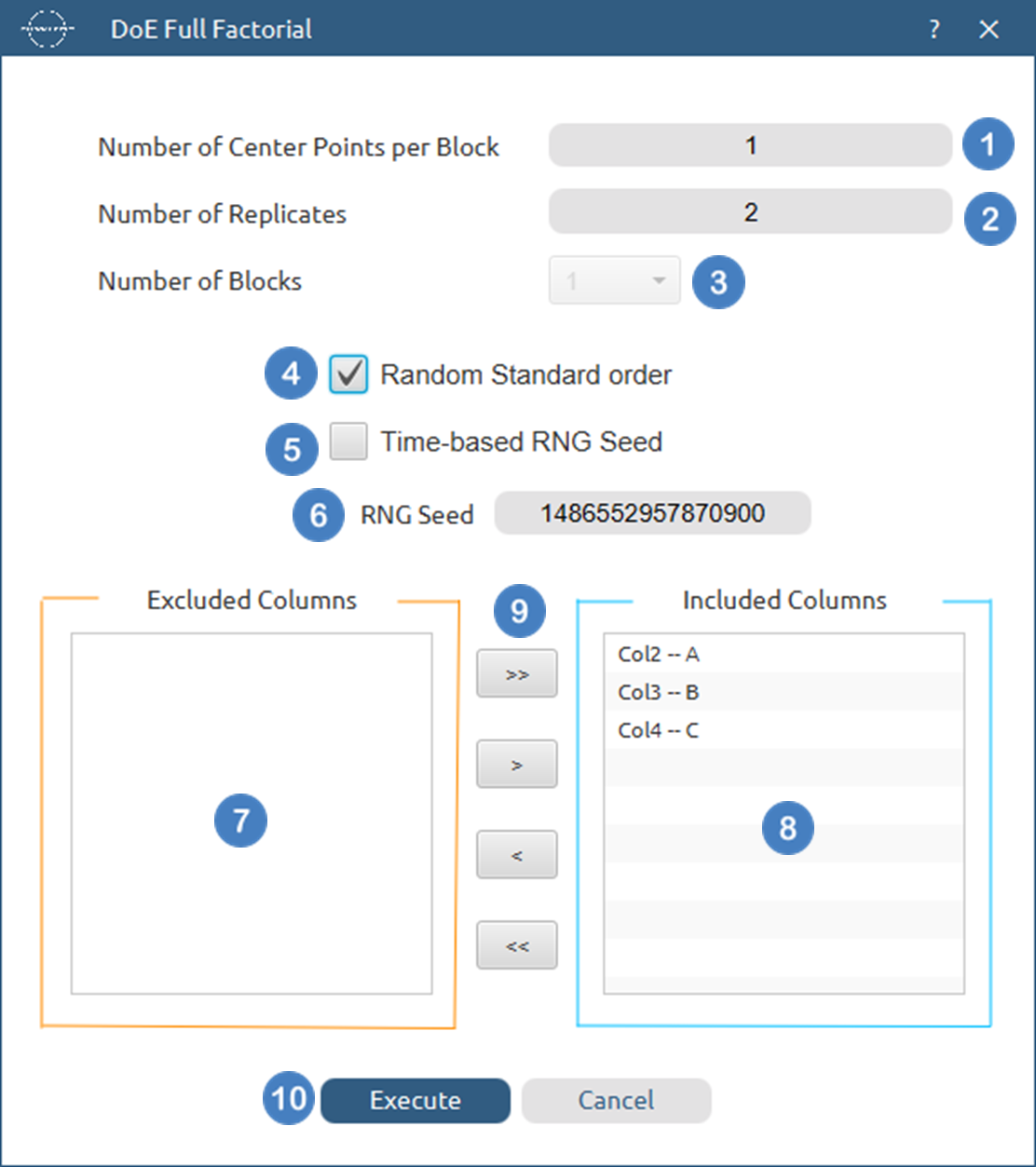
  1. Select DOE \(\rightarrow\) Factorial \(\rightarrow\) Full Factorial.
  2. Select the Number of Center Points [1] to be generated in the output list of experiments.
  3. Select the Number of Blocks [2]. The lowest value that can be set is 1.
  4. Select/tick if required the Random Standard order [3] to imply randomness in the output list of experiments.
  5. If randomness is selected either select/tick to generate the number seed for randomness based on time [4] or by manually setting a value [5].
  6. Select the columns by clicking on the arrow buttons [8] and moving columns between the Excluded Columns [6] and Included Columns [7] lists.
  7. Click on the Execute button [9] to perform Full Factorial design method.
Full Factorial
Output

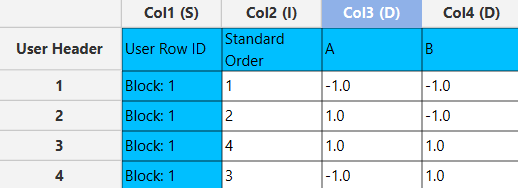
The output list of experiments is generated for the two factors outlining a list of 4 experiments based on the Full Factorial design. Block number is presented in Col1 as shown below and the standard order is provided in Col2.

Full Factorial output

References

  1. Box, G.E. and Behnken, D.W., Some new three level designs for the study of quantitative variables. Technometrics, 1960. 2(4): p. 455-475. doi.org/10.1080/00401706.1960.10489912.

  2. Box, G.E. and Wilson, K.B., On the experimental attainment of optimum conditions, in Breakthroughs in statistics: methodology and distribution. 1992, Springer. p. 270-310. doi.org/10.1007/978-1-4612-4380-9_23.

  3. Montgomery, Douglas C. Design and analysis of experiments. John wiley & sons, 2017.

  4. Speed, Terry. Statistics for Experimenters: Design, Innovation, and Discovery. 2006.

  5. Wu, CF Jeff, and Michael S. Hamada. Experiments: planning, analysis, and optimization. John Wiley & Sons, 2011.

Version History

Introduced in Isalos Analytics Platform v0.2.4

Instructions last updated on January 2025