Mixtures
Table of contents
Mixtures Design
Mixture design (experiment) is a special class of response surface method (RSM). These experiments focus on understanding how various proportions of components influence the overall characteristics of a mixture. A critical aspect of mixture experiments is that the factors being tested are the proportions of each component within the mixture. There’s an inherent constraint in these experiments: the sum of the proportions of all components must always equal 1. This constraint introduces unique challenges in both the design and analysis phases of the experiments.
Simplex Methods
To effectively address these challenges, two popular designs are often employed: the simplex lattice design and the simplex centroid design. The simplex lattice design offers a comprehensive approach by testing at all possible combinations of component proportions, including those at the vertices, edges, and faces of the simplex. This design allows for a detailed exploration of the interactions between components across the entire range of possible formulations.
In contrast, the simplex centroid design focuses on the centroid of each subspace of the simplex, including the overall centroid. This method is particularly beneficial for initial studies where a full-scale experimental approach may be impractical. It provides a more streamlined set of experiments that can still yield valuable insights into the main effects and some interactions among the mixture components.
Both the simplex lattice and simplex centroid designs are instrumental in overcoming the challenges posed by the fixed sum constraint in mixture experiments. They enable researchers to systematically explore and optimize different formulations, making them invaluable tools in the development of new products and processes where mixture proportions are critical. Although simplex lattice and simplex centroid are defined on the full simplex, they can still be used when simple bounds are present if those bounds can be absorbed by a reparameterization. Only when the constraints cannot be recast as an affine image of the simplex—for example, coupled linear inequalities or regions that are truncated/non-simplex—do lattice and centroid designs stop being appropriate; in those cases, constrained-mixture designs such as extreme-vertices or computer-generated optimal designs are needed.
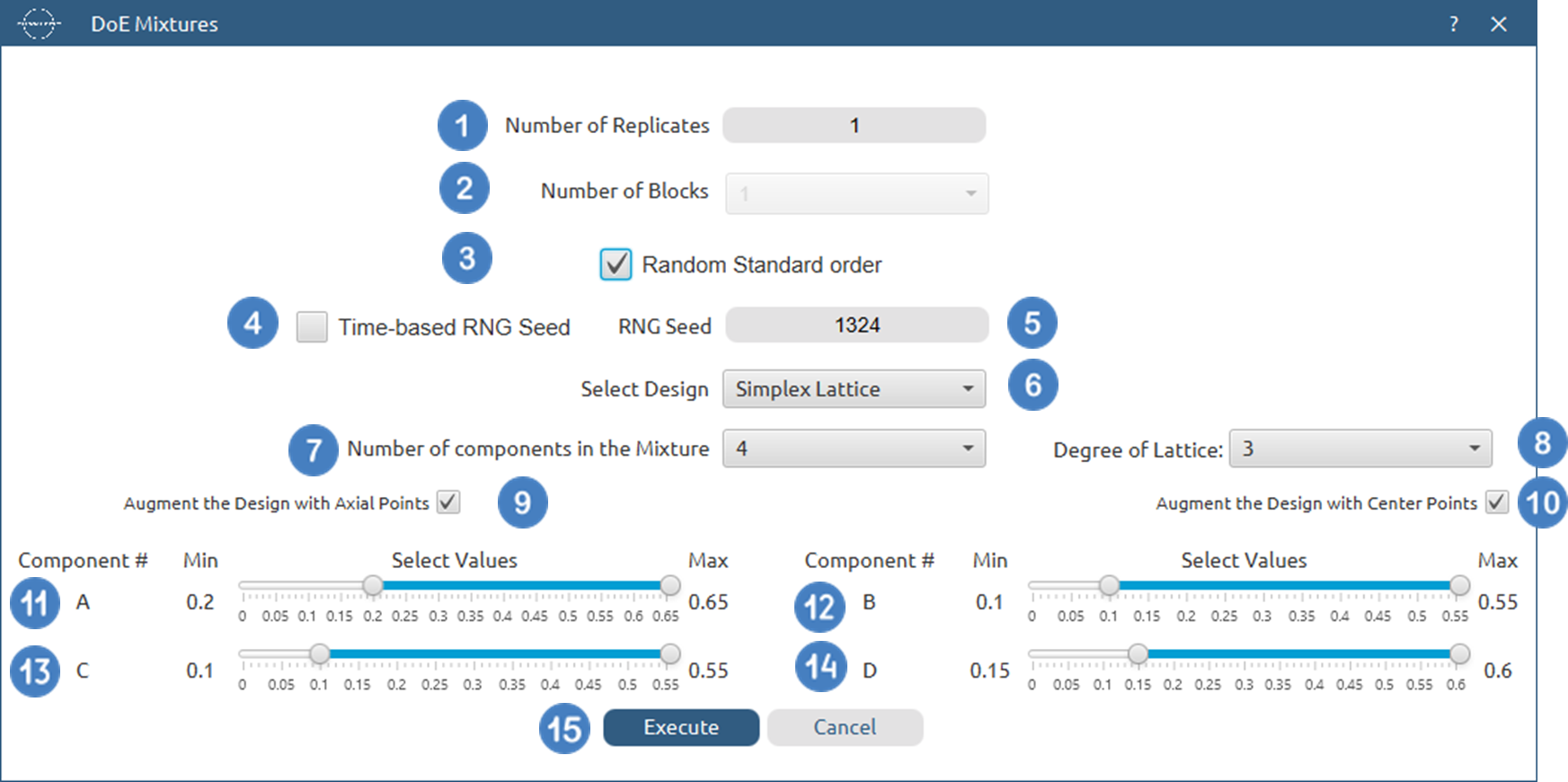
Use the Simplex Mixture function by browsing in the top ribbon:
| DOE \(\rightarrow\) Mixtures \(\rightarrow\) Mixtures Design |
And then selecting one of the two Simplex Methods
Input
Input data for Mixtures design is not required.
Configuration
| Number of Replicates | Select manually the Number of Replicates which represents the number of times to replicate the entire design. This value should be an integer, and the lowest acceptable value is 1. |
| Number of Blocks | Select from the list of available options the Number of Blocks. These designs can only be blocked on replicates, so the available options include 1 and the selected Number of Replicates. |
| Random Standard order | You can tick/select the box if randomness is required in the output list of experiments. |
| Time-based RNG Seed | If randomness is selected, then you have the option to also tick/select the box to set the random generated number seed based on time. |
| RNG Seed | Select manually the random generated number seed if required. |
| Select Design | Select Design offers two options either Simplex Centroid or Simplex Lattice. |
| Number of components | Select the Number of components (factors) from the drop-down list. |
| Degree of Lattice | If Simplex Lattice design is chosen, then select the Degree of Lattice from the drop-down list. |
| Augment the Design with Axial Points | Select/tick the box to Augment the Design with Axial Points if desired. |
| Augment the Design with Center Points | If Simplex Lattice design is chosen, then there is also the option to select/tick to Augment the Design with Center Points. |
| Component | Drag the horizontal value bars for each component to specify the min and max (composition) value for each component. |
Output
A list of experiments (combinations) is generated in the output datasheet along with the Block number, the Replicate Number, the Standard order and the Point type of each experiment based on the Mixtures design method selected.
Example
Input
No input data is required in the input datasheet.
Configuration
- Select
DOE\(\rightarrow\)Mixtures\(\rightarrow\)Mixtures Design. - Select the
Number of Replicates[1]. The lowest value that can be set is 1. - Select the
Number of Blocks[2]. - Select/tick if required the
Random Standard order[3] to imply randomness in the output list of experiments. - If randomness is selected either select/tick to generate the number seed for randomness based on time [4] or by manually setting a value [5].
- Select Design to be either
Simplex CentroidorSimplex Lattice[6]. - Select
Number of componentsin the Mixture from the drop-down list [7]. - If Simplex Lattice design method is selected, then select the Degree of Lattice from the drop-down list [8].
- Select/tick to
Augment the Design with Axial Points[9]. - If
Simplex Latticedesign method is selected, then select/tick toAugment the Design with Center Points[10]. - Drag the horizonal value bars for each component to specify the min and max (composition) value for each component or enter them manually using the min and max text fields (which allow precision up to 1e-5) [11], [12],[13] and [14].
- Click on the
Executebutton [15] to perform Mixtures design method.
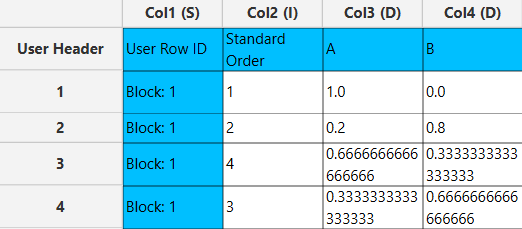
Output
The output list of experiments is generated for the two components outlining a list of 4 experiments based on the Mixtures design. Standard Order, Block number, Replicate Number and Point Type are presented in Cols 2,3,4 and 5 accordingly as shown below.
Extreme Vertices
When the feasible region defined by the constraints is not a simplex, a different strategy is needed to generate design points. A widely used option is the Extreme Vertices (EV) approach. EV first enumerates the vertices of the feasible polytope (the intersection of the mixture simplex with the linear constraints) and then augments them with informative interior points—typically face centroids up to a user-specified dimension and optional axial points (moves from a centroid toward individual vertices within the feasible region). The method supports arbitrary linear constraints among component proportions.
When general linear constraints are present, design points are computed via the CONSIM algorithm; otherwise, the XVERT algorithm is used. Regarding face centroids: For a mixture with q components, a d-dimensional face is a subspace where exactly d components are free to vary and the remaining q-d components are fixed at their face-defining values (often bounds or zeros). The centroid of such a face can be constructed by assigning the fixed components their required values and distributing the remaining mass equally among the d free components.
In addition to face centroids, a single “grand centroid” is often added; in this implementation it is taken as the arithmetic mean of all computed extreme vertices, providing a central interior point within the feasible region.
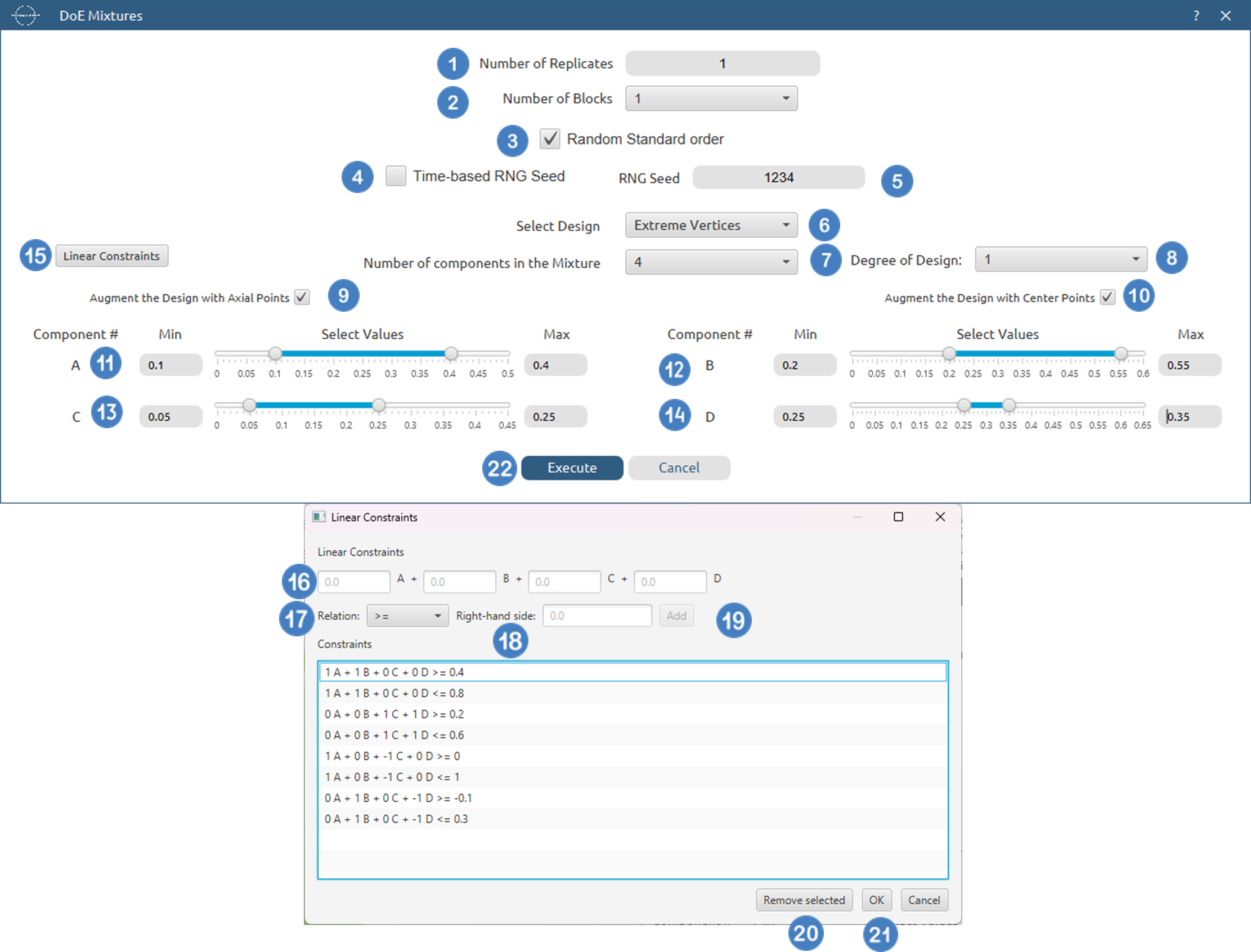
Use the Extreme Vertices Mixtures function by browsing in the top ribbon:
| DOE \(\rightarrow\) Mixtures \(\rightarrow\) Mixtures Design |
And then selecting the Extreme Vertices Design.
Input
Input data for Mixtures design is not required.
Configuration
| Number of Replicates | Select manually the Number of Replicates which represents the number of times to replicate the entire design. This value should be an integer, and the lowest acceptable value is 1. |
| Number of Blocks | Select from the list of available options the Number of Blocks. These designs can only be blocked on replicates, so the available options include 1 and the selected Number of Replicates. |
| Random Standard order | You can tick/select the box if randomness is required in the output list of experiments. |
| Time-based RNG Seed | If randomness is selected, then you have the option to also tick/select the box to set the random generated number seed based on time. |
| RNG Seed | Select manually the random generated number seed if required. |
| Select Design | Select the Extreme Vertices option as the design |
| Number of components | Select the Number of components (factors) from the drop-down list. |
| Degree of Design | Select the degree up to which to add face centroids. |
| Augment the Design with Axial Points | Select/tick the box to Augment the Design with Axial Points if desired. |
| Augment the Design with Center Points | Select/tick the box to Augment the Design with Center Points if desired. |
| Linear Constraints | Click this option to insert linear constraints for the proportions of components. |
| Component | Drag the horizontal value bars for each component to specify the min and max (composition) value for each component. |
Output
A list of experiments (combinations) is generated in the output datasheet along with the Block number, the Replicate Number, the Standard order and the Point type of each experiment based on the Mixtures design method selected.
Example
Input
No input data is required in the input datasheet.
Configuration
- Select
DOE\(\rightarrow\)Mixtures\(\rightarrow\)Mixtures Design. - Select the
Number of Replicates[1]. The lowest value that can be set is 1. - Select the
Number of Blocks[2]. - Select/tick if required the
Random Standard order[3] to imply randomness in the output list of experiments. - If randomness is selected either select/tick to generate the number seed for randomness based on time [4] or by manually setting a value [5].
- Select Design to be
Extreme Vertices[6]. - Select
Number of componentsin the Mixture from the drop-down list [7]. - Select the
Degree of Designfrom the drop-down list [8]. - Select/tick to
Augment the Design with Axial Points[9]. - Select/tick to
Augment the Design with Center Points[10]. - Drag the horizonal value bars for each component to specify the min and max (composition) value for each component or enter them manually using the min and max text fields (which allow precision up to 1e-5) [11], [12],[13] and [14].
- Optionally specify
Linear Constraints[15] by inputting the coefficient[16] for each component, the relation[17] of the constraint and the right-hand side coefficient[18] and then clickingAdd[19]. If a constraint needs to be removed select it and use theRemove Selected[20] button. After inserting all constraints click onOK[21] - Click on the
Executebutton [22] to perform Extreme Vertices design method.
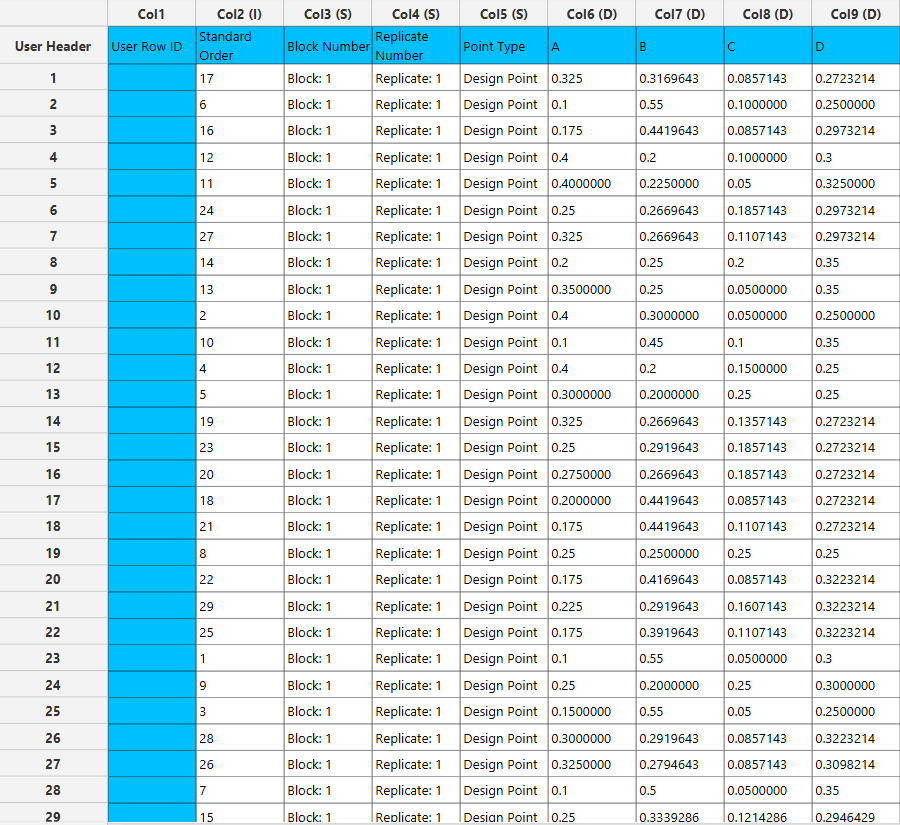
Output
The output list of experiments is generated for the two components outlining a list of 4 experiments based on the Extreme Vertices design. Standard Order, Block number, Replicate Number and Point Type are presented in Cols 2,3,4 and 5 accordingly as shown below.
References
-
Box, G.E. and Behnken, D.W., Some new three level designs for the study of quantitative variables. Technometrics, 1960. 2(4): p. 455-475. doi.org/10.1080/00401706.1960.10489912.
-
Box, G.E. and Wilson, K.B., On the experimental attainment of optimum conditions, in Breakthroughs in statistics: methodology and distribution. 1992, Springer. p. 270-310. doi.org/10.1007/978-1-4612-4380-9_23.
-
Montgomery, Douglas C. Design and analysis of experiments. John wiley & sons, 2017.
-
Speed, Terry. Statistics for Experimenters: Design, Innovation, and Discovery. 2006.
-
Wu, CF Jeff, and Michael S. Hamada. Experiments: planning, analysis, and optimization. John Wiley & Sons, 2011.
-
Snee, Ronald D. “Experimental designs for mixture systems with multicomponent constraints.” Communications in Statistics-Theory and Methods 8, no. 4 (1979): 303-326. doi.org/10.1080/03610927908827762.
-
Piepel, Gregory F. “Programs for generating extreme vertices and centroids of linearly constrained experimental regions.” Journal of Quality Technology 20, no. 2 (1988): 125-139. doi.org/10.1080/00224065.1988.11979093.
-
Snee, Ronald D., and Donald W. Marquardt. “Extreme vertices designs for linear mixture models.” Technometrics 16, no. 3 (1974): 399-408. doi.org/10.1080/00401706.1974.10489209.
Version History
Introduced in Isalos Analytics Platform v0.2.4
Instructions last updated on November 2025