Robust Parameter

Robust parameter design (RPD) is a crucial technique within the broader context of response surface methods, aimed at optimizing process settings to achieve desirable outcomes under varying conditions. In robust parameter design, the primary objective is to find factor settings that not only produce a mean response within specified limits but also minimize the response variability due to noise factors. Noise factors are variables that cannot be controlled during normal operation but significantly affect the process outcome. By controlling these noise factors during a process robustness study, it becomes possible to understand how fluctuations in these factors influence the response under different settings of the controllable factors.

The methodology typically involves fitting a second-order model for the controllable factors to capture the curvature of the response surface accurately. Additionally, the first-order effects and interactions of noise factors with controllable factors are modelled. These interactions are crucial as they help in understanding how changes in controllable factors can mitigate the effect of noise, thereby making the process more robust.

From the robust parameter design, two new models are developed. One model predicts the mean of the response as a function of the controllable factors, while the other predicts the variance. Notably, noise factors do not explicitly appear in these models; however, the parameter estimates for the interactions between control and noise factors critically influence the shape of the response surface for variance.

The Taguchi method is a well-known approach within robust parameter design, popularized for its structured way of studying the effects of multiple noise factors. Taguchi’s key contribution is the use of orthogonal arrays to systematically analyze the effects of noise and control factors, reducing the number of experiments needed to gather sufficient data. This method places a strong emphasis on cost-effectiveness and efficiency in experimental design.

Combined array designs, often associated with Taguchi methods, involve the simultaneous consideration of both control and noise factors in a single experimental setup. This approach enables the experimenter to assess the interaction effects directly and is particularly useful in complex processes where interactions between control and noise factors are significant.

Both Taguchi methods and combined designs underscore the philosophy of robust design: optimizing product performance and quality under a range of operating conditions by systematically controlling and examining variability. These methodologies are integral to developing products and processes that are consistently reliable and meet customer expectations in the real world.

Use the Robust Parameter design function by browsing in the top ribbon:

DOE \(\rightarrow\) Robust Parameter

Table of contents

  1. References
  2. Version History

Input

Numerical values should be specified in the input datasheet. Minimum of three columns (factors) should be specified as the minimum requirement for performing Robust Parameter design calculation is to have at least two control factors and one noise factor. Two levels/values should be specified for each factor (column) as minimum requirement.

Configuration

Number of Blocks Select manually the Number of Blocks. The lowest value that can get is 1.
Random Standard order You can tick/select the box if randomness is required in the output list of experiments.
Time-based RNG Seed If in the randomness is selected, then you have the option to also tick/select the box to set the random generated number seed based on time.
RNG Seed Select manually the random generated number seed if required.
Taguchi Design Select/tick the radio button corresponding to Taguchi Design if required.
Combined Design Select/tick the radio button corresponding to Combined Design if required.
Noise Factor/Available Columns/Control Factor Select manually from the Available Columns using the buttons the required columns which to be specified as control factors to the Control Factor dialog box and the one that required to be specified as noise factors to the Noise Factor dialog box.

Output

A list of experiments (combinations) is generated in the output datasheet along with the Block number and the Standard order based on the Robust Parameter design method selected.

Example

Input

In the input datasheet minimum requirement is to specify three factors (columns) and insert minimum two levels (values) for each factor (column), as shown below.

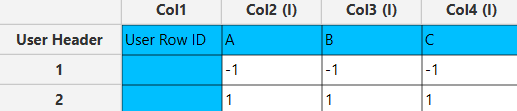
Robust Parameter input

Configuration

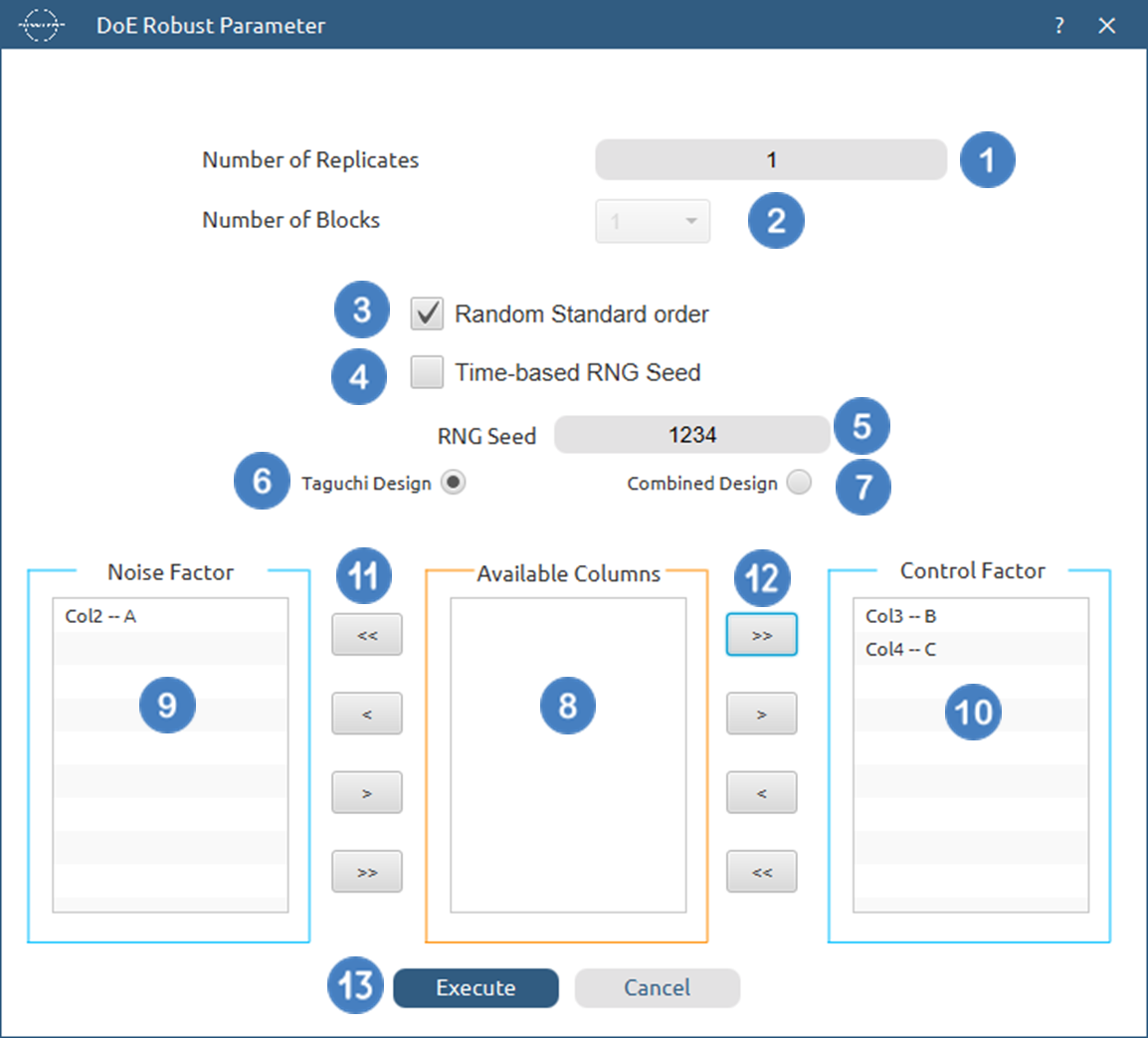
  1. Select DOE\(\rightarrow\) Robust Parameter.
  2. Select the Number of Blocks [1]. The lowest value that can be set is 1.
  3. Select/tick if required the Random Standard order [3] to imply randomness in the output list of experiments.
  4. If randomness is selected either select/tick to generate the number seed for randomness based on time [4] or by manually setting a value [5].
  5. Select/Tick either the Taguchi Design [5] radio button or the Combined Design [6] radio button.
  6. Select the columns from the Available Columns window [7] that correspond to noise factors by using the arrows [10] to move them to the Noise Factor window [8] and the one that correspond to control factors by using the arrows [11] to move them to the Control Factor window [9].
  7. Click on the Execute button [12] to perform `Robust Parameter design method.
Robust Parameter

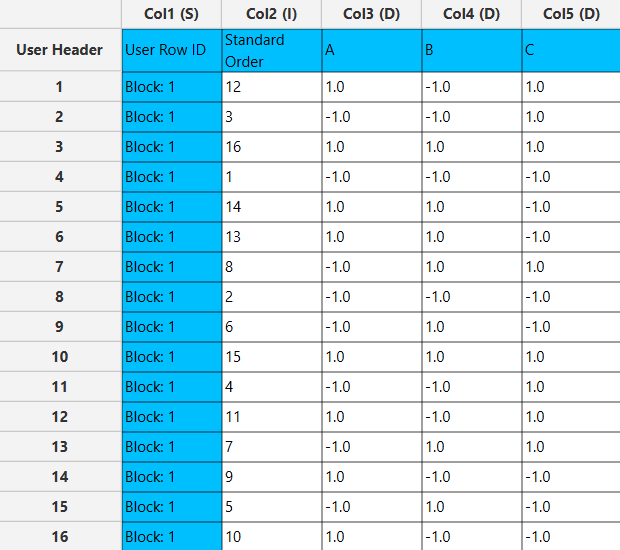
Output

The output list of experiments is generated for the two control factors and one noise factor outlining a list of 16 experiments based on the Robust Parameter Taguchi design. Block number is presented in Col1 as shown below and the standard order is provided in Col2.

Robust Parameter Output

References

  1. Box, G.E. and Behnken, D.W., Some new three level designs for the study of quantitative variables. Technometrics, 1960. 2(4): p. 455-475. doi.org/10.1080/00401706.1960.10489912.

  2. Box, G.E. and Wilson, K.B., On the experimental attainment of optimum conditions, in Breakthroughs in statistics: methodology and distribution. 1992, Springer. p. 270-310. doi.org/10.1007/978-1-4612-4380-9_23.

  3. Montgomery, Douglas C. Design and analysis of experiments. John wiley & sons, 2017.

  4. Speed, Terry. Statistics for Experimenters: Design, Innovation, and Discovery. 2006.

  5. Wu, CF Jeff, and Michael S. Hamada. Experiments: planning, analysis, and optimization. John Wiley & Sons, 2011.

Version History

Introduced in Isalos Analytics Platform v0.2.4

Instructions last updated on January 2025