Response Surface

Response Surface Designs are a subset of Design of Experiments (DoE) aimed at optimizing a response variable by exploring the relationships between multiple factors and their interactions. These designs are used when the goal is to find the optimal settings for factors that lead to the best outcome, and they are usually used as a next step after performing a screening design to reduce the number of parameters included in the model. By fitting a mathematical model to experimental data, response surface designs allow researchers to map out a surface that represents the response’s behavior across factor levels.

Table of contents

  1. Box Behnken
  2. Central Composite
  3. References
  4. Version History

Box Behnken

Box-Behnken1 designs are an integral component of response surface methodology (RSM) in experimental statistics, tailored for optimizing systems with multiple interacting variables. Renowned for their efficiency, these designs effectively capture interactions among variables while avoiding some of the complexities and potential pitfalls of full factorial designs.

A defining feature of Box-Behnken designs is the assignment of each factor to one of three equally spaced values: typically coded as -1, 0, and +1. These values correspond to the low, medium, and high levels for each factor, respectively. Such systematic placement of factors facilitates a comprehensive exploration of the response surface by allowing for a detailed investigation into how different factor levels influence the outcome.

Crucially, Box-Behnken designs are structured to fit a quadratic model. This capability is particularly valuable because it accommodates not only linear relationships but also the interaction effects (products of two factors) and squared terms of the factors. This adaptability makes Box-Behnken designs suitable for experiments where complex interactions between factors are anticipated, and where the response to changes in factor levels may be non-linear.

Another significant advantage of Box-Behnken designs is their ability to maintain a reasonable ratio of experimental points to coefficients in the quadratic model, typically ranging from 1.5 to 2.6. This balance is crucial for managing both computational complexity and the predictive accuracy of the model. By optimizing this ratio, the design maximizes the information obtained from each experimental run, enhancing the efficiency of the study.

Furthermore, Box-Behnken designs aim to minimize the variation in estimation variance, which depends solely on the distance from the center of the design space. This characteristic is particularly evident in designs with four and seven factors, where it helps ensure the reliability of results and maintains low variance across the smallest (hyper)cube encompassing all experimental points.

In summary, Box-Behnken designs offer an optimal trade-off between the completeness of information gathered and the experimental effort required. This makes them a sophisticated yet practical choice for exploring and understanding complex experimental landscapes, especially in scenarios where multiple variables interact in potentially nonlinear ways.

Use the Box Behnken function by browsing in the top ribbon:

DOE \(\rightarrow\) Response Surface \(\rightarrow\) Box Behnken

Input

In the input data sheet, numerical values should be specified with minimum 3 columns and two values each representing min and max level of each factor (column).

Configuration

Number of Center Points Select manually the Number of Center Points to be included in the output list of experiments. There is no minimum requirement or any other limitation.
Number of Blocks Select manually the Number of Blocks. The lowest value that can get is 1.
Random Standard order You can tick/select the box if randomness is required in the output list of experiments.
Time-based RNG Seed If in the randomness is selected, then you have the option to also tick/select the box to set the random generated number seed based on time.
RNG Seed Select manually the random generated number seed if required.
Include/exclude columns Select manually the columns through the dialog window: Use the buttons to move columns between the Included Columns and Excluded Columns list. Single-arrow buttons will move all selected columns and double-arrow buttons will move all columns.

Output

A list of experiments (combinations) is generated in the output datasheet along with the Block number based on the Box Behnken design method.

Example

Input

In the input datasheet in the right-hand side, you can specify minimum of three factors (columns) and minimum two levels/values (rows) for each factors representing min and max values, as shown below.

Box Behnken input
Configuration
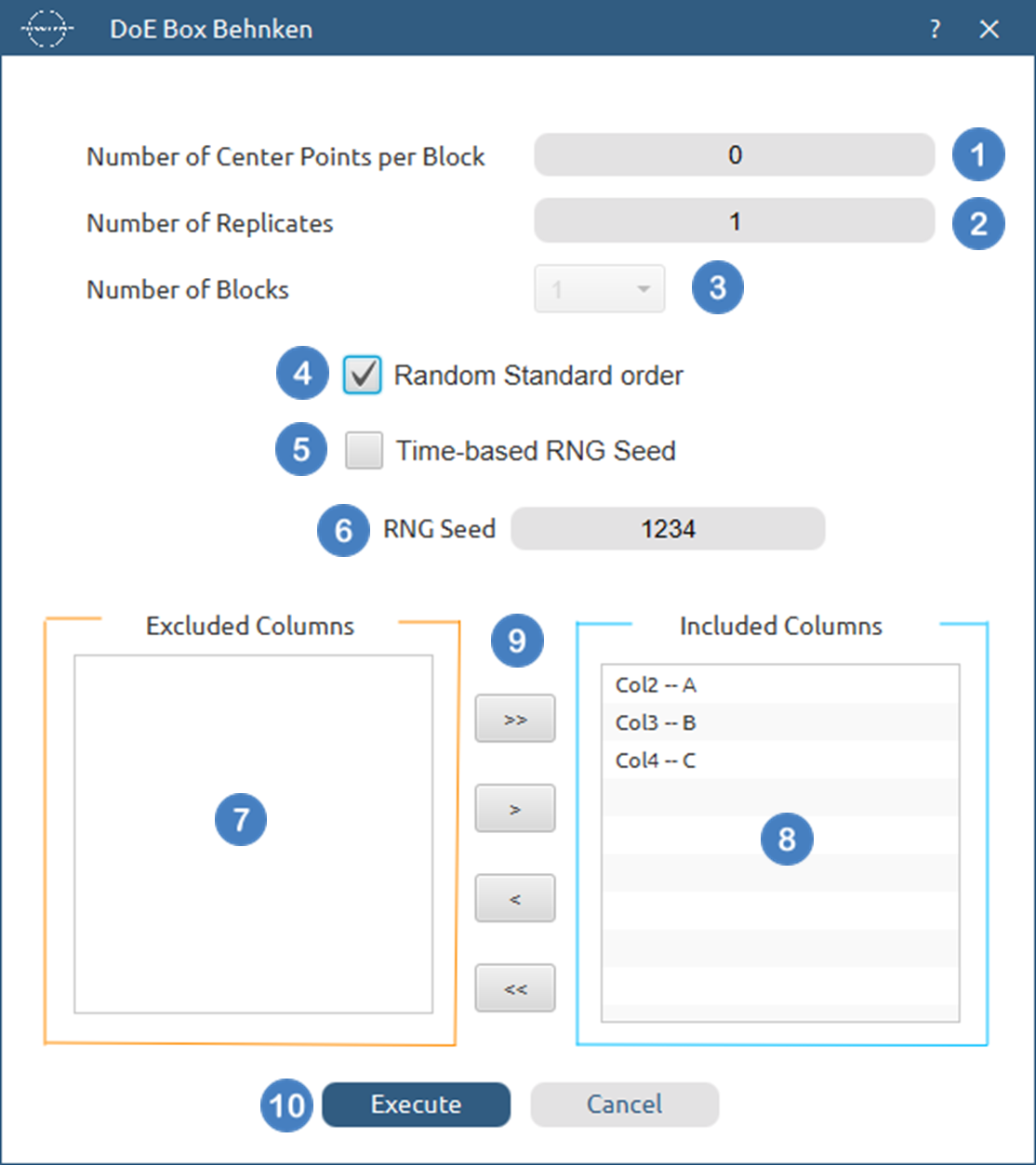
  1. Select DOE \(\rightarrow\) Response Surface \(\rightarrow\) Box Behnken.
  2. Type the Number of Center Points [1] to be generated in the output list of experiments.
  3. Type the Number of Blocks [2]. The lowest value that can be set is 1.
  4. Select/tick if required the Random Standard order [3] to imply randomness in the output list of experiments.
  5. If randomness is selected either select/tick to generate the number seed for randomness based on time [4] or by manually setting a value [5].
  6. Select the columns by clicking on the arrow buttons [8] and moving columns between the Excluded Columns [6] and Included Columns [7] lists.
  7. Click on the Execute button [9] to perform Box Behnken design method.
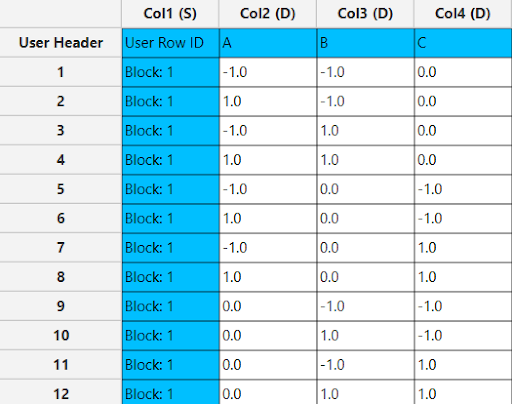
Box Behnken
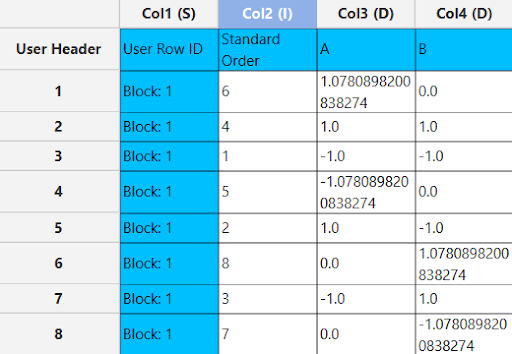
Output

The output list of experiments is generated for the three factors outlining a list of 12 experiments based on the Box Behnken design. Block number is presented in Col1 as shown below.

Box Behnken

Central Composite

The Central Composite Design (CCD), introduced by George E. P. Box and K. B. Wilson in 1951 and followed up by Box and Hunder in 1957,2 is a foundational technique in Response Surface Methodology (RSM) designed to explore the entire response surface of a process and locate the optimal response within that surface. The structure of CCD includes a factorial or fractional factorial design, augmented with center points and a set of “star points”. These star points are strategically placed along the axes of the factors under investigation at a distance that extends beyond the factorial points, crucial for estimating the curvature of the response surface. This design is adept at fitting a full quadratic model, capturing both the interactions between factors and their squared effects.

CCD is divided into three primary variations, each tailored to meet specific experimental needs and constraints:

  • Circumscribed Designs (CCC): This variant situates cube points at the corners of a unit cube defined by the product of intervals [-1,1]. It includes star points that may lie on or extend outside the cube and center points at the origin. The CCC is advantageous for its ability to explore beyond the confines defined by the factorial points, making it suitable for experiments where extending the range of factor levels is possible.
  • Inscribed Designs (CCI): In this design, the star points are scaled to the values of -1 and +1, placing them on the surface of the unit cube, while the cube points are located within the interior of the cube. The CCI is particularly beneficial when there are restrictions on the maximum or minimum factor levels that can be practically or safely tested, as it confines the experimentation within the standard levels.
  • Faced Designs (CCF): This approach positions the star points on the faces of the cube, rather than extending beyond or resting on the surface of the cube. This results in a design that utilizes only three levels per factor, as opposed to the five levels used in the circumscribed and inscribed designs. Faced designs are advantageous in scenarios where resources are limited or when there are constraints that prevent a more extensive exploration of factor levels.

Each of these designs is tailored to fit different experimental conditions and requirements, allowing researchers to choose based on the number of factors, the limitations on factor levels, the necessity to explore beyond the factorial space, and the resources available for conducting experiments. By providing a range of configurations, CCDs offer a flexible and robust framework for experimenters aiming to optimize processes and responses effectively.

Use the Central Composite function by browsing in the top ribbon:

DOE \(\rightarrow\) Response Surface \(\rightarrow\) Central Composite

Input

Numerical values should be specified in the input datasheet. The minimum requirement is to specify 2 columns (factors) along with two levels (values/rows) each representing min and max levels, respectively.

Configuration

Number of Center Points Select manually the Number of Center Points to be included in the output list of experiments. There is no minimum requirement or any other limitation.
Number of Blocks Select manually the Number of Blocks. The lowest value that can get is 1.
Random Standard order You can tick/select the box if randomness is required in the output list of experiments.
Time-based RNG Seed If in the randomness is selected, then you have the option to also tick/select the box to set the random generated number seed based on time.
RNG Seed Select manually the random generated number seed if required.
Select Design Choose among the options, ccc, ccf, cci representing circumscribed design, faced design and inscribed design, respectively.
Select alpha method If ccc or cci designs are previously selected, then select either orthogonal or rotatable design.
Include/exclude columns Select manually the columns through the dialog window: Use the buttons to move columns between the Included Columns and Excluded Columns list. Single-arrow buttons will move all selected columns and double-arrow buttons will move all columns.

Output

A list of experiments (combinations) is generated in the output datasheet along with the Block number and the Standard order based on the Fractional Factorial design method selected.

Example

Input

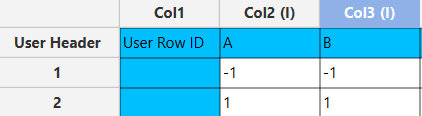
In the input datasheet minimum requirement is to specify three factors (columns) and insert minimum two levels (values) for each factor (column), as shown below..

Central Composite input
Configuration
  1. Select DOE \(\rightarrow\) Response Surface \(\rightarrow\) Central Composite.
  2. Select the Number of Center Points [1] to be generated in the output list of experiments.
  3. Select the Number of Blocks [2]. The lowest value that can be set is 1.
  4. Select/tick if required the Random Standard order [3] to imply randomness in the output list of experiments.
  5. If randomness is selected either select/tick to generate the number seed for randomness based on time [4] or by manually setting a value [5].
  6. Choose to Select Design [6] method among the options, ccc, ccf and cci representing circumscribed, faced and inscribed designs, respectively.
  7. If ccc or cci designs are previously selected, then Select alpha method [7] either to have orthogonal or rotatable design.
  8. Select the columns by clicking on the arrow buttons [10] and moving columns between the Excluded Columns [8] and Included Columns [9] lists.
  9. Click on the Execute button [11] to apply the Central Composite design method.
Central Composite
Output

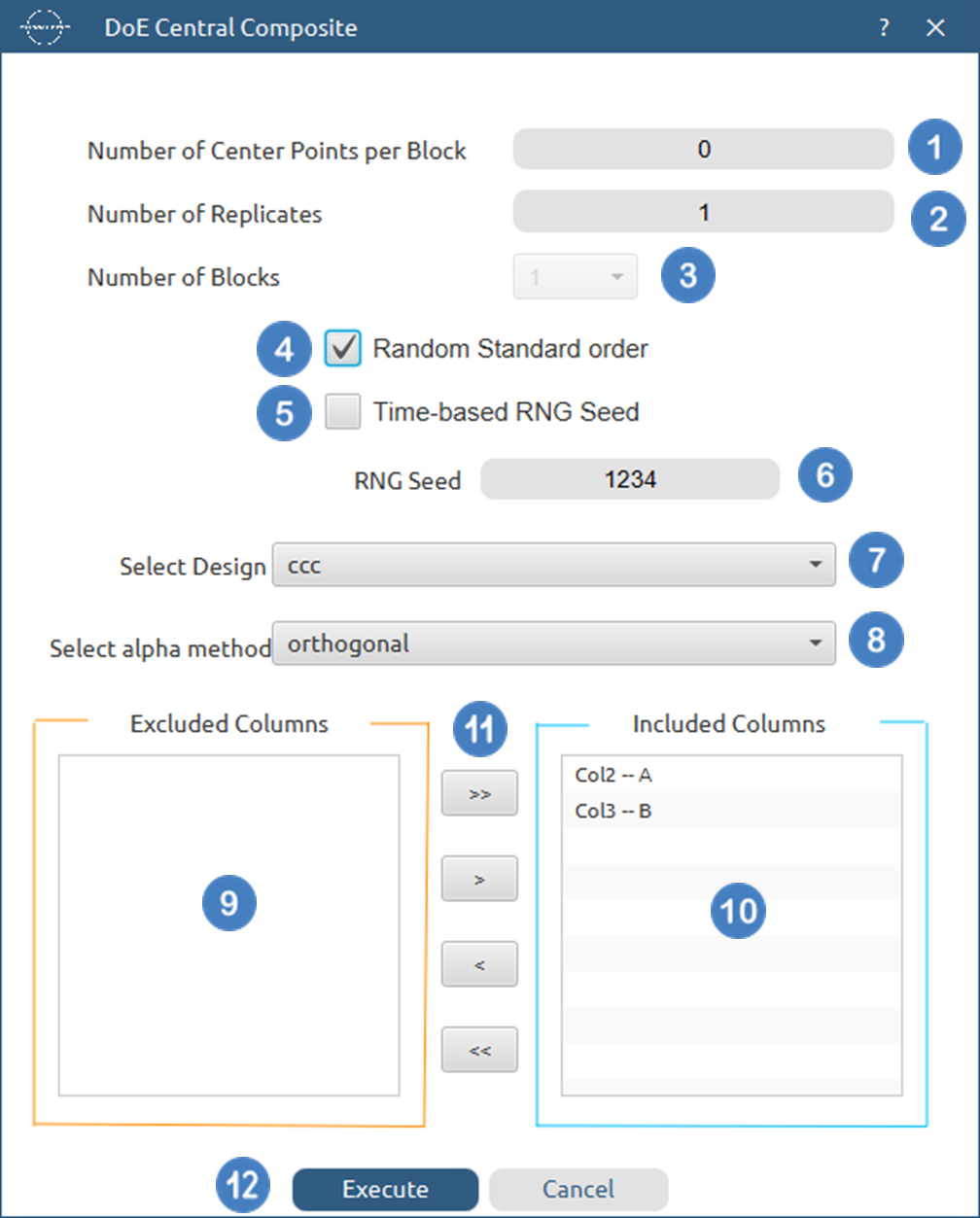
The output list of experiments is generated for the two factors outlining a list of 8 experiments based on the Central Composite Circumscribed (ccc) and orthogonal design. Block number is presented in Col1 as shown below and the standard order is provided in Col2.

Central Composite

References

  1. Box, G.E. and Behnken, D.W., Some new three level designs for the study of quantitative variables. Technometrics, 1960. 2(4): p. 455-475. doi.org/10.1080/00401706.1960.10489912.

  2. Box, G.E. and Wilson, K.B., On the experimental attainment of optimum conditions, in Breakthroughs in statistics: methodology and distribution. 1992, Springer. p. 270-310. doi.org/10.1007/978-1-4612-4380-9_23.

  3. Montgomery, Douglas C. Design and analysis of experiments. John wiley & sons, 2017.

  4. Speed, Terry. Statistics for Experimenters: Design, Innovation, and Discovery. 2006.

  5. Wu, CF Jeff, and Michael S. Hamada. Experiments: planning, analysis, and optimization. John Wiley & Sons, 2011.

Version History

Introduced in Isalos Analytics Platform v0.2.4

Instructions last updated on January 2025