Random Number Generator

Random numbers are widely used in data science and machine learning model development to mimic input data obtained from a uniform population where every number of the population has the same chance of selection.

Table of contents

  1. Tips
  2. See also
  3. References
  4. Version History

There are two options for generating random numbers in Isalos: decimal numbers between 0 and 1, and integer or real numbers between a user defined interval.

Decimal random number between 0 and 1

A decimal random number between $[0, 1)$ interval is selected according to a uniform probability distribution function. This means that the application of the Random Number Generator function for infinite times leads to a set of numbers satisfying the uniform probability distribution function (see Eq. 1).

$$ \begin{equation} f(x) = \begin{cases} 1, \: \mathrm{for} \: x \in \mathbb{R}\cap[0, 1) \\ 0, \: \mathrm{for} \: x \: \in \mathbb{R}\cap((-\infty, 0)\cup[1, +\infty)) \end{cases} \end{equation} {\qquad [1] \qquad} $$

where $x$ is the random number, and $f(x)$ is the uniform probability distribution function.

Integer random number between a user defined interval

An integer random number between $[a, b)$ interval is selected according to a uniform probability distribution function. This means that the application of the Random Number Generator function for infinite times leads to a set of numbers satisfying the uniform probability distribution function for the user defined interval (see Eq. 2).

$$ \begin{equation} f(x) = \begin{cases} \frac{1}{b-a}, \: \mathrm{for} \: x \in \mathbb{Z}\cap[a, b) \\ 0, \: \mathrm{for} \: x \: \in \mathbb{Z}\cap((-\infty, a)\cup[b, +\infty)) \end{cases} \end{equation} {\qquad [2] \qquad} $$

where $x$ is the integer random number, $f(x)$ is the uniform probability distribution function, and $a$ and $b$ are integer numbers that define the upper and the lower limit of the interval where the probability function is non-zero.

Real random number between a user defined interval

A real random number between $[a, b)$ interval is selected according to a uniform probability distribution function. This means that the application of the Random Number Generator function for infinite times leads to a set of numbers satisfying the uniform probability distribution function for the user defined interval (see Eq. 3).

$$ \begin{equation} f(x) = \begin{cases} \frac{1}{b-a}, \: \mathrm{for} \: x \in \mathbb{R}\cap[a, b) \\ 0, \: \mathrm{for} \: x \: \in \mathbb{R}\cap((-\infty, a)\cup[b, +\infty)) \end{cases} \end{equation} {\qquad [3] \qquad} $$

where $x$ is the real random number, $f(x)$ is the uniform probability distribution function, and $a$ and $b$ are real numbers that define the upper and the lower limit of the interval where the probability function is non-zero.

Use the Random Number Generator function by browsing in the top ribbon:

Statistics \(\rightarrow\) Random Number Generator

Input

No input data are needed to use the Random Number Generator function.

Configuration

Select Method Choose the method for the generated random number between the options: Default (Double Between (0,1)) and User Defined (user-defined interval).
Select Number Type Select between Integer Number and Double Number (real), when the User Defined method is selected.
From The lower limit $a$ of the interval. $a\in\mathbb{Z}$, when Integer Number is selected, and $a\in\mathbb{R}$, when Double Number is selected.
To The upper limit $b$ of the interval. $b\in\mathbb{Z}$, when Integer Number is selected, and $b\in\mathbb{R}$, when Double Number is selected.

Output

Data matrix with the generated random number. The user-selected method, and/or number type and interval limits are also presented in the output spreadsheet.

Example

Input

No input is needed in the left-hand spreadsheet of the tab.

Configuration
Decimal random number between 0 and 1
  1. Select Statistics [1] \(\rightarrow\) Random Number Generator [2].
random-browse
  1. Select the Default(Double Between (0,1)) method [3] from the Select Method dropdown list.
  2. Click on the Execute button [4] to generate the random number.
random-01-configuration
Integer random number between a user defined interval
  1. Select Statistics \(\rightarrow\) Random Number Generator.
  2. Select the User Defined method [1] from the Select Method dropdown list.
  3. Select Integer Number from the Select Number Type dropdown list [2] that will appear.
  4. Type the lower (From) [3] and the upper (To) [4] limits of the user defined interval (only integer values are allowed).
  5. Click on the Execute button [5] to generate the random number.
random-integer-configuration
Real random number between a user defined interval
  1. Select Statistics \(\rightarrow\) Random Number Generator.
  2. Select the User Defined method [1] from the Select Method dropdown list.
  3. Select Double Number from the Select Number Type dropdown list [2] that will appear.
  4. Type the lower (From) [3] and the upper (To) [4] limits of the user defined interval.
  5. Click on the Execute button [5] to generate the random number.
random-real-configuration
Output
Decimal random number between 0 and 1

In the right-hand spreadsheet of the tab the output random number [1] is presented as well as the selected method [2].

random-01-output
Integer random number between a user defined interval

In the right-hand spreadsheet of the tab the generated random number [1] is presented as well as the selected method [2], the number type [3], and the lower [4] and upper [5] interval limits.

random-integer-output
Real random number between a user defined interval

In the right-hand spreadsheet of the tab the generated random number [1] is presented as well as the selected method [2] the number type [3], and the lower [4] and upper [5] interval limits.

random-real-output

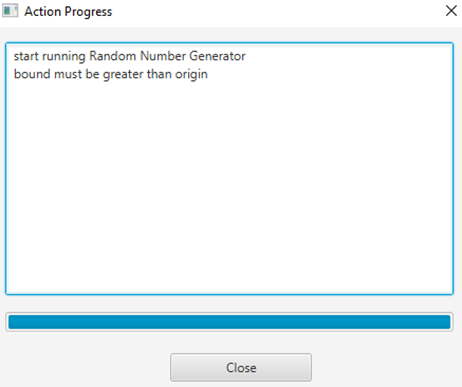
In case that the inserted lower limit is higher than the inserted upper limit then a message appears to inform you about this discrepancy.

random-error

Tips

The Random Number Generator is:

  • Useful to create unbiased samples/subgroups from uniform populations.
  • Required as input for stochastic methods and Monte Carlo calculations.
  • Useful to investigate randomness in a model

See also

The number generated by Random Number Generator can be applied as input in other functions of Isalos.

References

  1. Press, W. H., Vetterling, W. T., Teukolsky, S. A., & Flannery, B. P. (1988). Numerical recipes. Cambridge University Press, London, England. psu.edu.

Version History

Introduced in Isalos Analytics Platform v0.1.18

Instructions last updated on June 2024